Introduction
In high temperature electrochemistry a typical goal is to obtain a number of impedance sweeps performed on the sample at multitude of temperatures and or atmospheres. This process may take considerable amount of time and effort as it is typically controlled manually. In general the instruments (furnace and impedance spectrometer) do not communicate with each other, and the user must initiate the measurements when conditions are deemed suitable.
With Omega software the impedance sweeps can be automated and in this application note the process is briefly described.
Physical setup
This setup included Omega software running on a computer, ProboStat sample holder, impedance spectrometer and a furnace. The impedance spectrometer was connected to the sample holder, and the sample holder was placed inside the furnace. The computer was connected to both the furnace and the impedance spectrometer and the software controlled both devices according user specified instructions. The control thermocouple for the furnace is located next to the sample, so temperature read from the furnace is the actual sample temperature. This type of furnace with possibility for default thermocouple override simplifies the process.
The details of the setup and the connections are specified in the Omega and ProboStat manuals.
Software functionality
In general, the Omega software reads the furnace temperature periodically. A number of pre-defined sweeps wait for right conditions to occur. The conditions can simply be such as "The furnace temperature is higher/lower than x" (case 1), or as well more advanced, such as "599 ºC < Furnace temperature < 601 ºC AND Furnace temperature rate of change < +/- 0.1 ºC / min (for the last 30 minutes)" (case 2). On the latter case the sweep would only start after the temperature has properly stabilized, while the earlier would start the sweep even if the furnace temperature kept changing as in this picture. Both cases are covered below.
Case 1: Sweeps while temperature changes
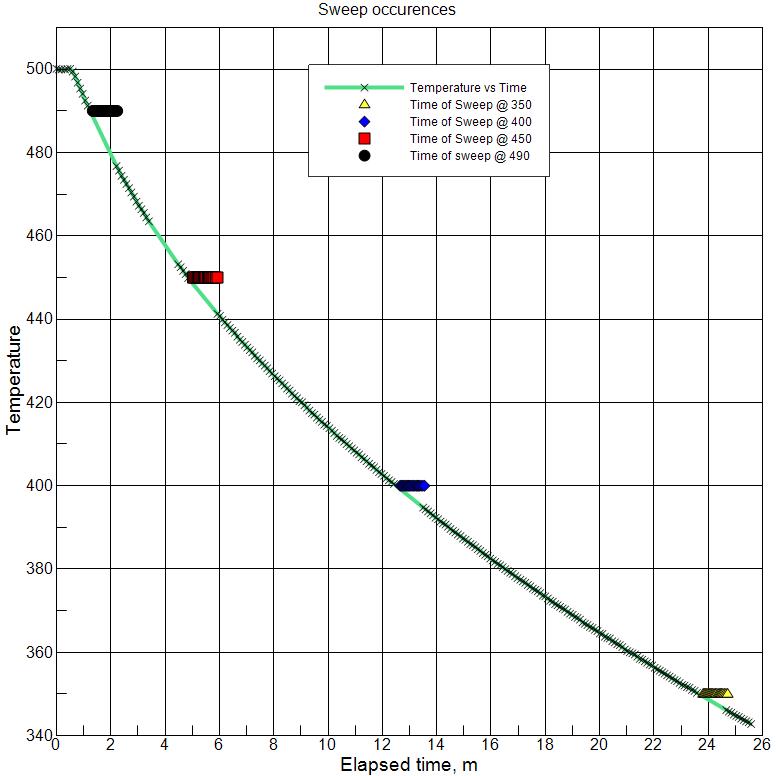
Fastest way to gather a number of impedance sweeps of the sample is to do so at constantly rising or declining temperature. In case of a sweep with 50 points, execution of such sweep takes about 1.5 minutes (if frequencies are above 1 Hz) and the change of temperature over the sample during this time may in some cases be considered negligible. If that is not the case, proceed to case 2.
|
|
Picture 1 Sweeps taken on a fast declining temperature where the cooling rate of a furnace is not restricted in any way. Note that this is not recommended behaviour and will put lot of thermal stress on ceramics across the temperature gradient, and is presented here just as a reference to demonstrate the (worst possible) change in the sample temperature during taking of a sweep. The short horizontal lines represent the time it took for the sweeps to perform and the sloped line represents the temperature measured at the sample. It is easy to see the temperature keeps changing during the sweeps (each of which consisted of 50 points of >1 Hz frequencies and lasted roughly 90 seconds each). The heating or cooling rate of a furnace can be set to any desired value, for example such as 5º C/min. In such conditions during a sweep the sample temperature would change approximately 7.5 ºC/min. As mentioned earlier this may or may not be acceptable. |
Case 2: Sweeps when temperature is stable
In case temperature needs to be stable when taking sweeps, the conditions determining when a sweep should start are slightly more complicated. Studying the stability of a measured property requires calculation of rate of change, and this can be achieved by utilizing the coefficient tool of the temperature series. In the Graph section add a serie for the temperature and add a coefficient tool (tick the linear regression checkbox) for that serie. The tool automatically calculates (with linear least squares) coefficient of the x last points of the series. This real time information can be used to determine when sweep should start.
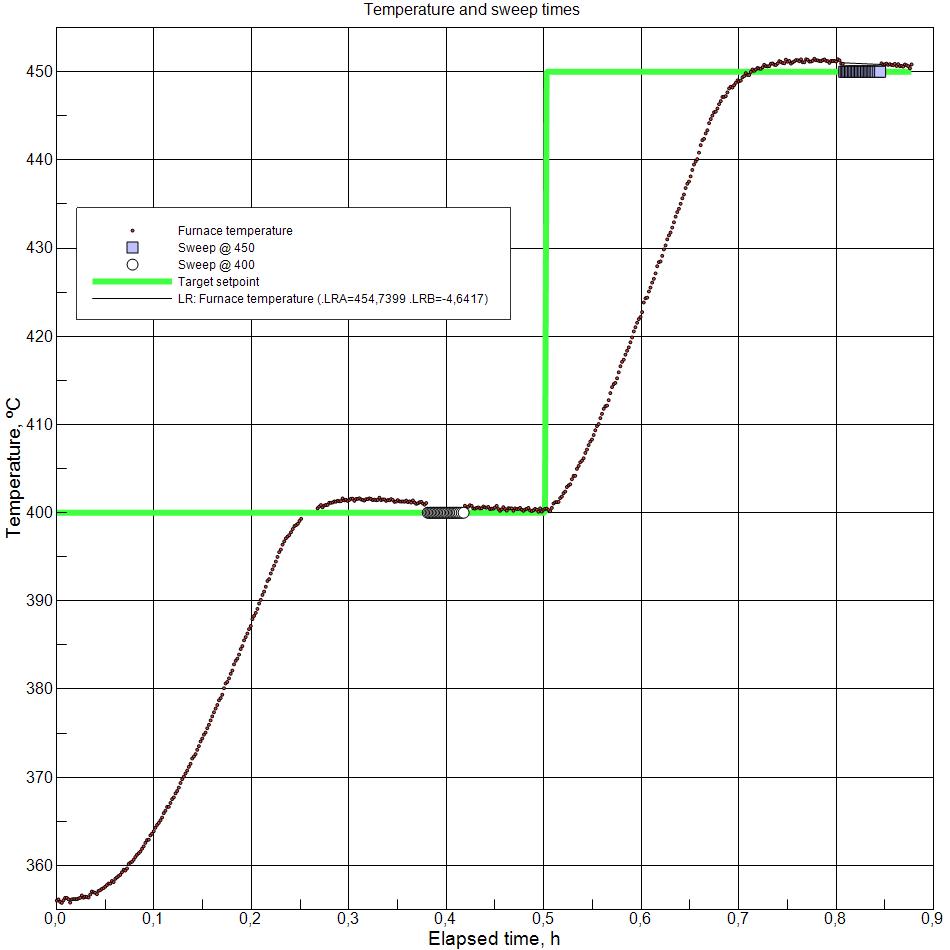 |
Picture 2 Furnace temperature was controlled with the software in steps of 50 ºC per every 30 minutes. The light green line represents the setpoint (target temperature) information sent to the furnace with ramp rate 5º C/min (desired rate of change in temperature). Series with small dots represent the measured furnace temperature. The big circles and squares represent the times when a sweeps were being performed. In addition to specific furnace temperature, the angle of last x point is used to determine when the furnace temperature rate of change is small enough. The unit of the rate of change is Y axis unit / X axis unit, and in this case ºC were plotted against hours. The starting condition for 'sweep at 400' was (399 ºC < Furnace temperature < 401 ºC) AND (rate of change < +/- 15 ºC/hour). In detail this was written: ($N1.ET>399)&($N1.ET<401)&($S1.LRB<15)&($S1.LRB>-15) where the & symbol equals the AND mathematical operator, the $N1.ET represents the measured temperature of the furnace, and $S1.LRB is the slope of the linear least squares coefficient of the series 'Furnace temperature' plot. The unit of the plot is degrees per hour, so LRB can be used as it is with no conversion to minutes etc. For the Linear regression tool, the LRA is the offset in units of Y axis and LRB is slope in units of Y axis per X axis. (Units are relevant since the X axis can be minutes, hours, days, dates, or maybe even not time related at all.) After the Sweep is done, we aim to go to a new temperature, and for simplicity, this is here done time dependent. It can also be done just studying if the sweep has finished, but time dependency is easier for this example. New setpoint gets sent to furnace each time the expression TRUNC(EHOUR($N1.TI)*2)*50+400 evaluates to a new value. EHOUR($N1.TI) returns elapsed time since the beginning of the measurement, and TRUNC drops the fractional part of a number. So every 60 minutes this returns the next integer (since we multiply by 2 we twice as often, every 30 minutes). This is multiplied by 50, and 400 added, thus getting stepped setpoints from 400 onwards with step of 50, applied every 30th minute. For this the user must know roughly how long the ramp will take and how long it will take for the temperature to stabilize. Now, an important notice here is that the furnace temperature is not the same as the sample temperature. Moreover, stable sample temperature is not the same thing as stable samnple conditions. Depending on the sample and used atmosphere, the sample may need long time to reach chemical equilibrium. Better than testing for stable temperature would be to test for stable conductivity. And when the conductivity has proven stable, the sweeps are made and then sent to new temperature. This, obviously cannot be made with time dependent furnace control, instead before going to new temperature, the automation must evaluate if the sweep has been finished or not. Setup guide for Automatic sweeps as function of conductivity Please note that the actual sweep data is presented on the next image.
|
Representing the gathered data
Data from each performed sweep can be plotted on separate or shared graphs.
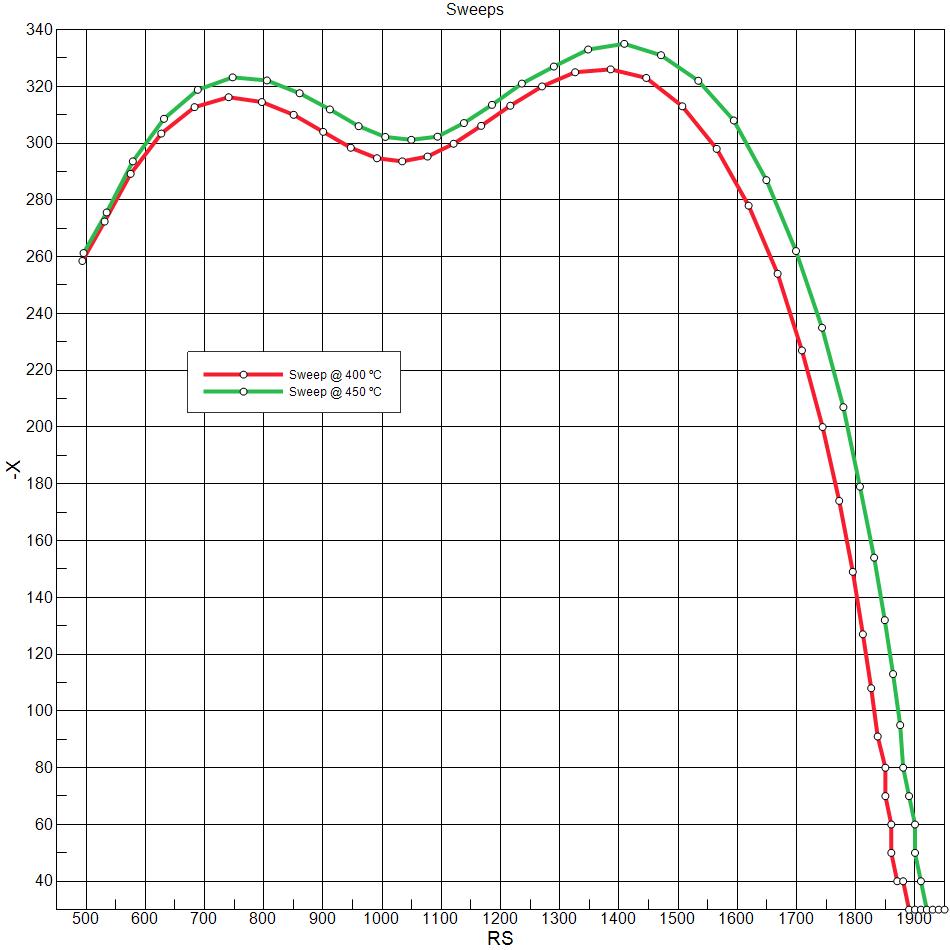 |
Picture 3 The sweep data itself can be plotted separately. |